数据结构与算法

排序查找算法

Posted by lily on April 7, 2023

刷题顺序参考：

数组——>链表——>哈希表——>字符串——>栈与队列——>树——>回溯——>贪心——>动态规划——>图论——>高级数据结构

学习思维导图

v2-9b19241550c3617d373c99e55bc56b44_r.jpg

时间复杂度和空间复杂度

时间复杂度

  • 概念：用于评估代码运行所需要时长的衡量单位
    • O(1),一段代码运行一个单位数量级
    • O(n),一层n次的循环
    • O(n^2)，两层循环嵌套，一共循环了n^2次
    • O(logn),也可以写作log2n，循环次数不固定，刚开始是n的循环，接下来每次循环都会导致循环次数减半。 
      while n>1:      #输入n = 64
  print(n)    #循环本要执行64次
  n = n//2    #结果在循环内部，循环减半，n减半变为32，循环需要执行32次..
  • 时间复杂度排序
    • 时间复杂度高的式子运行时间比时间复杂度低的运行得慢
    • O(1)<O(logn)<O(n)<O(nlogn)=O(logn^2)<O(n^2)<O(n^3)

      线性表的查找

  • 按顺序依次往后查找
  • 时间复杂度：每次查找，循环减半,时间复杂度为O（logn） ```python class Solution(object): def search(self, nums, target): left = 0 right = len(nums) - 1 while left<=right: #还存在可查找空间 mid = (left + right)//2 #中间值索引为左边+右边整除2（中心偏左） if nums[mid] == target: return mid elif nums[mid] > target: #查询值在mid左边,左边界不动，移动右边界 right = mid - 1 else: left = mid + 1 else: return -1 #查询不到返回-1

# 排序

- 常见排序算法：
   - LowB排序算法：冒泡（bobble）排序，选择（select）排序，插入（insert）排序
   - NB排序算法：快速排序，堆排序，归并排序
   - 其他算法：希尔排序，计数排序，基数排序
## 冒泡排序

- 时间复杂度：O(n^2),两层循环 ，每次循环长度都为列表长度n。
- ![image.png](https://cdn.nlark.com/yuque/0/2022/png/1238904/1659148601626-33c5b79a-8c73-45fc-ba88-4d5c98d43d27.png#averageHue=%23f7f7f7&clientId=u6ecd76ff-5a44-4&errorMessage=unknown%20error&from=paste&height=228&id=u23740031&name=image.png&originHeight=342&originWidth=237&originalType=binary&ratio=1&rotation=0&showTitle=false&size=12173&status=error&style=none&taskId=u4f984a75-5231-4f73-bd9e-bcfa496dbe9&title=&width=158)
### 基本特点：

- 时间复杂度：O(n^2)
- **每排一轮，都会让有序区多一个数。**
- **原地排序：在原有列表上的基础上排序修改调整列表**
1. 外层循环控制这样冒泡的操作要来回几趟
2. 内层循环控制每一趟相邻两个数之间的比较
3. 外层循环长度：由于列表有n个数，需要把n-1个数冒泡上去（剩下最小的数自然就沉到了第0位），所以需要循环n-1趟。
4. 内层循环长度：从第0位开始，用i0与i1进行比较；接着i1与i2进行比较；最后一位是i(n-1)与in进行比比较，所以内层循环指针应该最后指向第n-1，所以内层循环长度为n-1.
- 代码：
```python
def bobble_sort(list):
    for i in rang(len(list)-1):
        for j in rang(len(list)-1):
            #如果前一位的数大于后一位的数
            if list[j]>list[j+1]:
                #则交换位置
                list[j],list[j+1] = list[j+1],list[j]
            '''如前一位的数不大于后一位的数，这俩数不用交换位置，
            内层循环继续往前走，检查下两位相邻数字需不需要交换顺序'''
 #如果这一趟下来所有的数位次都不用交换，则说明列表已经排好了，
 #外层循环可以不用再继续了，所以可以用一个标志检验这一层循环是否
 #已经有序
def bobble_sort_verion2(li):
    for i in rang(len(li)-1):
        exchang = True
        for j in rang(len(li)-1):
            if li[j] > li[j+1]:
                li[j],li[j+1] = li[j+1],li[j]
                exchang = False
         if exchang:#说明内层循环一次也没交换过，可以退出循环了
            return

选择排序

  • 时间复杂度：O(n^2)
  • 图解：

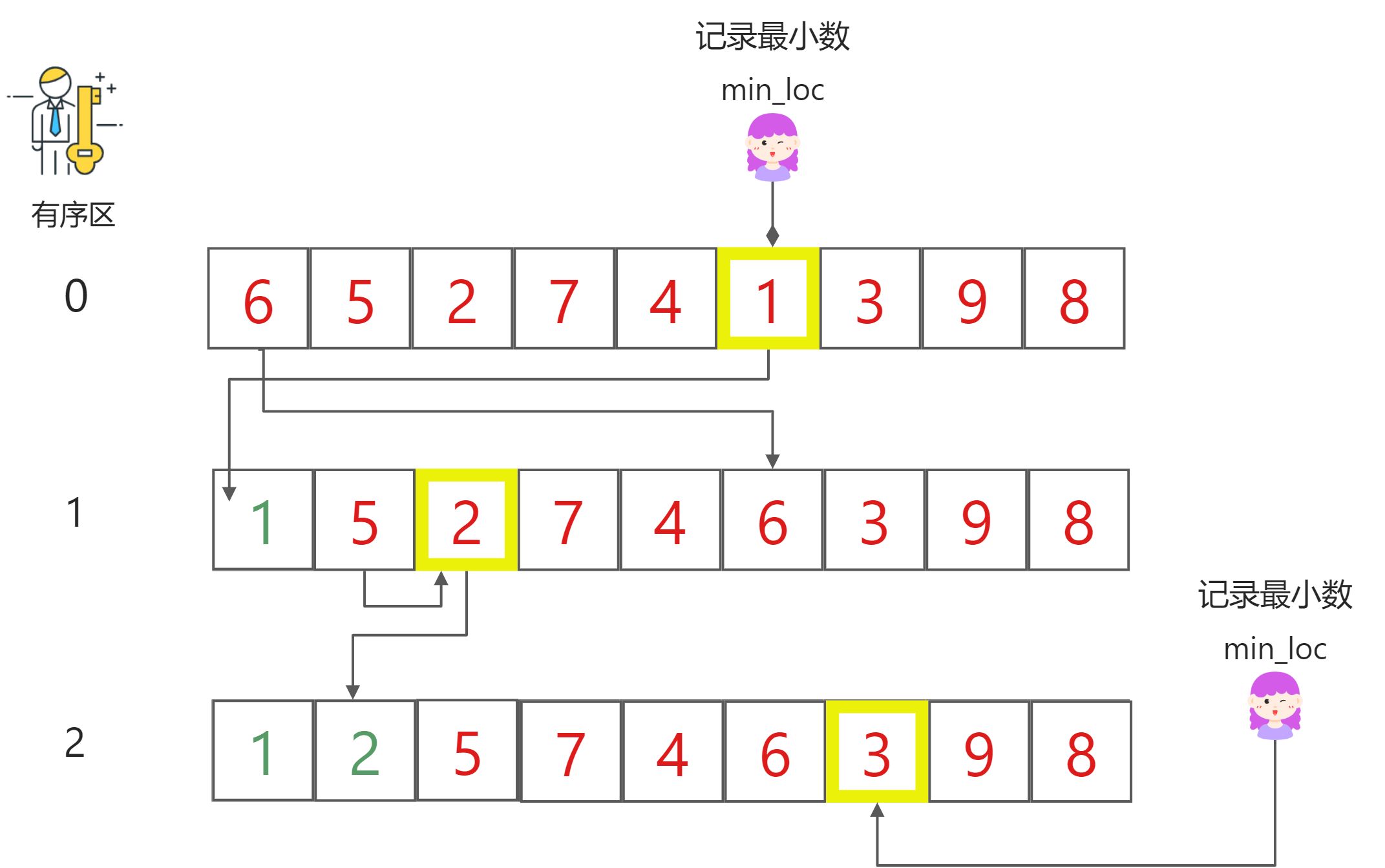
基本特点

  • 排序特点：把列表中最小的数找到，并放置（与第一个位置的数进行交换）到第一个位置上，直接挑出（select）最小的数与第一个位置数交换，不像冒泡排序，只与相邻的数比较且交换
    1. 遍历逻辑：在无序区中进行遍历，找到[无序区]最小数放入[有序区]的最后一位；有序区每新增一个数（每排好一遍），无序区遍历的起始位置就要向前挪一位。
    2. 核心步骤：
    1. 第一层遍历变量 i：
      1. 【i】表示有序区有多少个数，也表示下一个即将加入有序区数的索引
      2. 找到无序区开始处** i 最小数**下标x，记录该下标x
      3. 把x位置上的数放到 i 的位置上
    2. 第二层遍历变量 j ：
  • 代码实现 ```python def select_sort(li): for i in range(len(li)-1): #最后一个数不用排 # 找到当前最小的数 min_loc = i for j in range(i+1, len(li)): if li[j] < li[min_loc]: #直至找到最小的数 min_loc = j li[i], li[min_loc] = li[min_loc], li[i] ‘'’return li 不论是否return原来函数已经改变’’’

## 插入排序

- 时间复杂度：
- 图解：![image.png](https://cdn.nlark.com/yuque/0/2022/png/1238904/1659513264413-a47bfc32-5f9d-4f35-a6c9-3bf247be0699.png#averageHue=%23f4eeea&clientId=ue21e1b20-e4a1-4&errorMessage=unknown%20error&from=paste&height=115&id=u0a63be67&name=image.png&originHeight=172&originWidth=412&originalType=binary&ratio=1&rotation=0&showTitle=false&size=9874&status=error&style=none&taskId=ucfa971cf-cfa1-4d8f-b3b2-d04e6c5c10c&title=&width=274.6666666666667)
### 算法特点

1. 像打扑克牌一样把乱序的牌从头开始**选择插入的位置**，从而进行排序
2. 主要对‘’**有序区‘’**进行操作，把后续未知大小的牌一张一张**插入**‘’**有序区**‘’
3. 一比较完就要交换位置，才能实现每一张符合条件的牌逐次向后移
4. 一个遍历**记录**程序现在运行（操作、排序）到何处，另一个遍历**操控**某张牌该如何 比较，并**最后**决定插入到哪个位置
5. 代码实现
```python
def insert_sort(li):
    for i in range(len(li)-1):
        pick_car = i+1  # 对下一张牌进行操作
        while pick_car >= 1 and li[pick_car] <= li[pick_car-1]:
            li[pick_car], li[pick_car - 1] = li[pick_car - 1], li[pick_car]
            pick_car -= 1

快速排序(quick_sort)

外层循环条件不能一直保障内层循环条件

  • 一般情况下时间复杂度：** O(nlog**n**)**

image.png 涉及到递归，假设列表长度为16假设每一层都刚好把要排序的部分分割成两份，那么需要4层递归才能把所有的数排好顺序，24 = 16 ——>递归层数为 4 = log216 ——> logn，每层递归都要进行一次遍历列表长度n 所以粗略来算时间复杂度为 n*logn

基本逻辑

一步步建立有序关系

  1. 用partition函数先归位第一个元素_tmp_（左右有序）
  2. 设计递归函数依次归位其余元素（每个元素都左右有序），完成排序。

归位partition函数的设计

  1. 右指针right移动，从右向左一直找到比_tmp_小的数放到left（此时tmp位置即为left位置）位置上，停止移动。
  2. 左指针left移动，从左向右比对直到找到比_tmp_大的数放到right的位置上，停止移动。

一些边界条件

  1. 小循环中设置**left<right ** ：
  2. data[right] >= tmp **小循环时遇上与tmp值相等的元素：当left与right未重合，但data[left] == data[right]**（left位与right位的数大小相同时），进不了小循环，left与right的值不能改变，又出不了大循环，此时会造成死循环。

图解：

  • 保存要固定元素
  • 逐步赋值并覆盖元素，以达到交换左右元素的目的
  • 把固定元素放回最后的空位

image.png 代码实现：

def partition(data, left, right):
    tmp = data[left]
    while left < right:
        左边有空位，先从右边找元素补到左边
        '''直到找到符合条件的数再换位置，没找到就一直循环'''
        while left < right and data[right] >= tmp:
            right -= 1
        data[left] = data[right]
        '''找到大于tmp的数放到右边'''
        while left < right and data[left] <= tmp:
            left += 1
        data[right] = data[left]
    '''最后right == left后tmp归位'''
    data[left] = tmp
    return left

_内层循环有无 left < right 的区别 _

data = [1,2,3,0]

def partition1(data, left, right):
    tmp = data[left]
    while left < right:
        while data[right] > tmp:
            right -= 1
        data[left] = data[right]
        while data[left] < tmp:
            left += 1
        data[right] = data[left]
    data[left] = tmp
    return data

'''输出
[3, 0, 1, 2]'''

def partition2(data, left, right):
    tmp = data[left]
    while left < right:
        while left < right and data[right] > tmp:
            right -= 1
        data[left] = data[right]
        while left < right and data[left] < tmp:
            left += 1
        data[right] = data[left]
    data[left] = tmp
    return data

'''输出
[0, 1, 3, 2]'''

def quick_sort(data,left,right):
   '''数据由传入函数参数获得
    left = 0
    right = len(data) - 1'''
    if left < right:  #递归终止条件
        #返回分割位置
        posi = partition(data, left, right)
        #调整posi左边
        quick_sort(data, left, posi-1)
        #调整posi右边
        quick_sort(data, posi+1, right)

快排最坏情况

  1. 递归深度限制
  2. 时间复杂度最坏情况

堆排序（heap_sort）

树知识前传

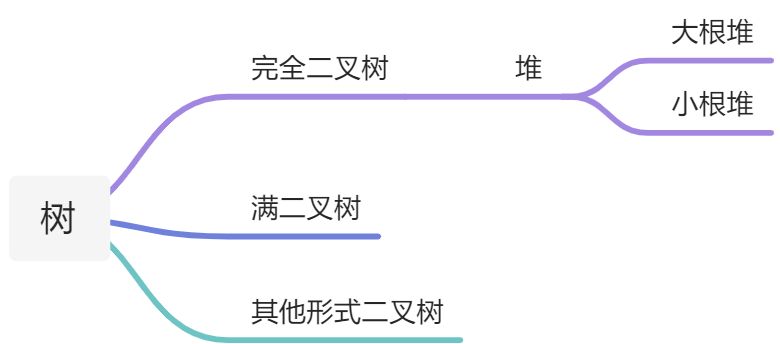
树：父亲节点与子节点的关系

  • 用数组来维护一棵完全二叉树
  • 知道父亲找孩子如果父亲节点在数组中索引为i，则左孩子为 ：left_child =ｉ＊ 2 +1；右孩子为：right_child = left_child + 1 = i * 2 + 2
  • 直到孩子找父亲 不管是左孩子还右孩子，父亲节点索引都为：i =（ child - 1） // 2 (在python中”//”为向下取整)。
  • 最后一个非叶子节点（父亲节点），列表长度为n， i = n//2 -1

    堆image.png

    根节点比子节点大的部分树结构或树结构为大根堆，构造大根堆或小根堆的过程叫做构造堆（heap）

基本逻辑

  • 时间复杂度：
  • image.png
    1. 构建堆
    1. 按照每一个父亲节点上的数都比子节点大进行构造，构造出来的堆在列表显示出部分有序
      1. 从上往下进行堆调整
    2. 使得堆在列表显示出全都有序
  • 代码实现： 
    def sift(li, low, high):
  # 自上向下调整函数,调整为大根堆
  i = low
  j = i*2 + 1 # 左孩子
  tmp = li[i] # 保存要调整的数
  while j <= high:
      # !!如果右孩子存在且大于左孩子!!
      if j + 1 <= high and li[j] < li[j+1]:
          j = j + 1 # 让j指向更大的孩子
      if li[j] > tmp:
          # 若子节点比 tmp大，可把子节点往上提，继续向下一层检索
          li[i] = li[j]
          i = j
          j = i*2 + 1
      else:
          # 直到子节点到合适的位置退出循环
          break
  li[i] = tmp

    def heap_sort(li):
  # 建造堆:从第一个非叶子节点开始从后向前局部调整
  deep = len(li)
''' 第一个非叶子节点可以从它的子节点反获取得到，
  它的孩子是列表里的最后一个数'''
  for leaf1 in range(deep//2-1, -1, -1):
      sift(li, leaf1, deep-1)
        
  # 排序堆：把最大数弹出后又调整生成最大数于根结点处
  for i in range(deep-1, -1, -1):
      # i 一直指向列表的最后一位，即指向最后一个叶子节点
  ''' 大根堆建造好后根节点数就是最大数，
   可以开始循环把最后一个数换到根节点上'''
  # 而最下面的位置则会依次被换成放置下来的最大数
      li[0], li[i] = li[i], li[0]
#  此时最低位i已经指向不用调整的最大数，所以最低位置为i-1
      sift(li, 0, 1-1)

topk问题——排序讨论

  1. 构建小根堆——最后排出来的数是由大到小的
    1. 时间复杂度O(nlogk)，需要遍历一次整个列表，每次遍历到的那个数都有可能进入小根堆里进行调整，假若每个数都会调整一次，那么调整时间复杂度为O（logk），所以总的时间复杂度为O(nlogk)
  2. 冒泡排序——冒前k个数上去——不需要排所有的数
    1. 时间复杂度：O(nk)，每次冒泡都会把最大的数冒到顶端去，要冒k个数，单个数都要花费O（n）的时间，所以总计时间复杂度为O（nk）
  • 如何用堆排序解决前k个大的数问题
    1. 从需要维护数据里获得前k个数，建立一个大小为k个数的小根堆。
    1. 此时堆顶为这k个数里面最小的数，即为第k大的数
      1. 遍历需要维护数据余下的数（列表里取出的前k个数之后的数），每次获取到的数与堆顶数进行比较，若大于堆顶数则进入小根堆进行调整，否则继续遍历下一个数。
    2. 调整即为维护小根堆的特性
      1. 遍历结束之后维护的小根堆里就是前k个数，逆序弹出就可以获得从大到小排列的前k大的数。
        • leetcode例题：前k个频率最高的数

归并排序(merge_sort)

😥归并思想

统计元素个数（元素计数）

  • 假设列表里有大量重复且无序的数，如何高效统计每个元素出现的频率

    手写count函数

    内置count模块再转换为元组等连续数据存储

    哈希表存储

CATALOG
    FEATURED TAGS
    JAVASE JavaWEB Spring python基础 学习工具 数据结构与算法 爬虫学习 计算机网络 springBoot BugNotice springSecurity projectLearning SQL
    FRIENDS