- 主流的数据结构与必须要掌握的算法思想
数据结构与算法简介
- 程序 = “数据结构”+“算法”
- 数据结构是程序实现的工具
- 算法是动态的存在于程序运行的过程
- 数据结构表达了多种数据间的关系
基本数据结构
- 逻辑结构:线性结构、树、图
- 物理结构:数据结构在实际代码中的实现
刷题顺序参考:
数组——>链表——>哈希表——>字符串——>栈与队列——>树——>回溯——>贪心——>动态规划——>图论——>高级数据结构
学习思维导图

时间复杂度和空间复杂度
时间复杂度
- 概念:用于评估代码运行所需要时长的衡量单位
- O(1),一段代码运行一个单位数量级
- O(n),一层n次的循环
- O(n^2),两层循环嵌套,一共循环了n^2次
- O(
logn),也可以写作log2n,循环次数不固定,刚开始是n的循环,接下来每次循环都会导致循环次数减半。while n>1: #输入n = 64 print(n) #循环本要执行64次 n = n//2 #结果在循环内部,循环减半,n减半变为32,循环需要执行32次..
- 时间复杂度排序
- 时间复杂度高的式子运行时间比时间复杂度低的运行得慢
- O(1)<O(logn)<O(n)<O(nlogn)=O(logn^2)<O(n^2)<O(n^3)
线性结构
列表
- 列表存储数据:连续存储
- 列表与数组的2点区别
- 列表的内存存放与c中数组存放的区别
- python中列表存放数据的地址
- c中数组直接存放数据
- 按下标索引: a[2] —–> id(a[2]) = id(a[0]) + 2*4
- 32位的机器中整数占4字节
- 列表的删除、插入、新增是如何实现的,时间复杂度是多少
数据结构
栈(Stack)

- 用列表来实现栈
- 栈只能在一端进行操作,后进先出,只能在列表末端进行插入和删除操作
- push:添加元素
- pop:删除栈顶元素
- get top:查看栈顶元素
- 括号匹配问题
class Stack(self):队列(Queue)

- 队列的实现方法——用py自带模块 ```python from collections import deque
que1 = deque(maxlen=10) que1.append(1) #队首进队(右边) que1.append([2,3]) #可以添加列表 que1.popleft() # 队尾出队(左边) ‘'’双向队列,左边为尾,右边为首’’’ que1.appendleft(4) #队尾进队(左边) que1.pop() #队首出队(右边) ‘'’当加入元素超过列表长度之后,队尾自动出队’’’
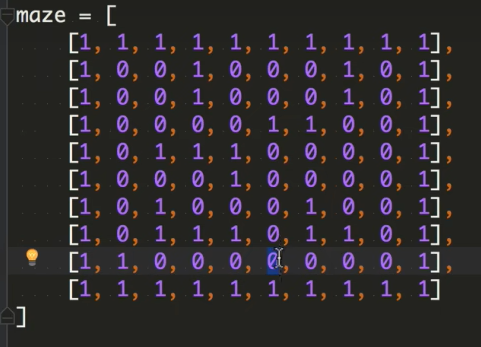
- 迷宫问题
- 深度优先搜索(回溯法)
- 广度优先搜索(可以找到最短路径,同时出发,第一个结束)
- 
# 双指针法
## 移除数组元素
```java
int i = 0;
int menberID = target;
for (int j = 0; j < total; i++, j++) {
p = team[j];
while (j<total && p == memberID) {
j++;
}
//team数组后面几位是置空的 team[j] == null
//无论置空为否, 都要把后面元素的值复制到前面来
team[i] = team[j];
}
//退出条件满足之时(j < total),i的值理应是total,
//但由于又进循环进行了一次判断,所以i多加了1
total = i-1;
滑动窗口:
当需要查找数组内某段_长度不固定且满足某些条件的数时,需要边遍历边控制窗口内的数,找到这些满足条件的长度不固定的数_
- example1:
**给定一个二进制数组 nums , 计算其中最大连续 1 的个数。**
**输入:**nums = [1,1,0,1,1,1]
**输出:**3
**解释:**开头的两位和最后的三位都是连续 1 ,所以最大连续 1 的个数是 3.
res = 0
slow, fast = 0, 0
while fast < len(nums):
if nums[fast] == 1:
fast += 1
continue
res = max(res, fast - slow)
# fast跳过0的情况,且时不用计算res值
while fast<len(nums) and nums[fast] == 0:
fast += 1
slow = fast
return max(res, fast - slow)
- 统一边界条件:当快指针指向0还是下一个值1的时候,慢指针指向哪里
- 慢指针如何移动
- 什么时候可以计算长度:当快指针指向0还是下一个值1的时候进行计算长度
KMP算法
见笔记KMP算法总结篇
